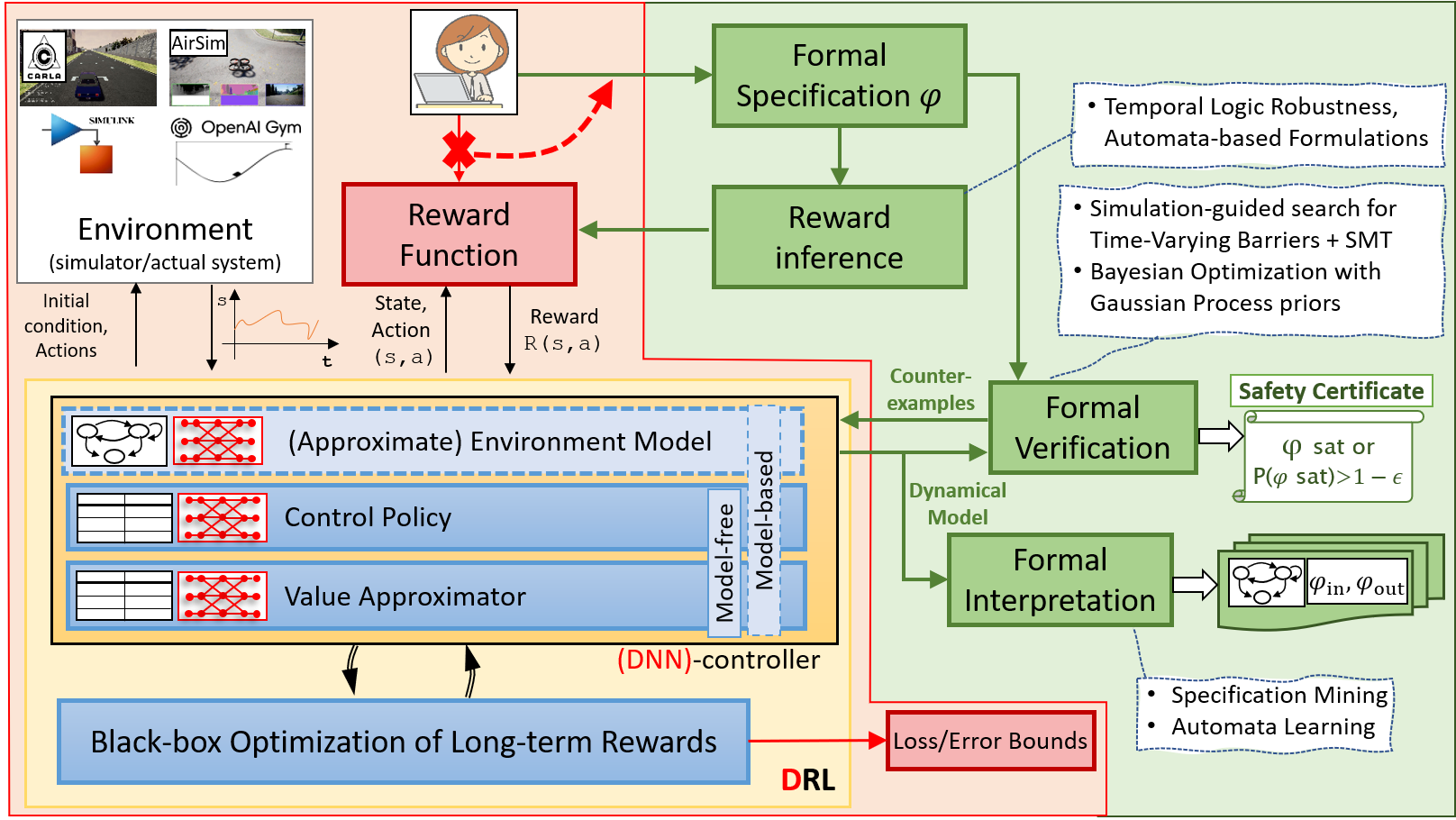
(Deep) Reinforcement Learning consists of a promising new class of techniques that aspire to solve control problems for highly uncertain and nonlinear environments, as well as train agents that can rival human decision-making. RL techniques fundamentally depend on defining a reward function that maps every agent state (or configuration) to some value. RL techniques assume that reward functions express desired behavior; i.e. agent policies that maximize rewards correspond to agent behaviors that are desired. However, for safety-critical system, ill-defined rewards can lead to behaviors that maximize rewards yet are undesirable or unsafe. We explore the problem of defining high-level formal specifications for systems and automatically inferring state-based reward functions from these. While these new class of RL algorithms that we will invent can certainly push the system towards maximizing rewards (and ergo satisfying the intended specification), there is no guarantee in deep RL of obtaining provably correct policies. A part of this project will explore formal methods and statistical approaches to prove the correctness of a discovered RL policy.
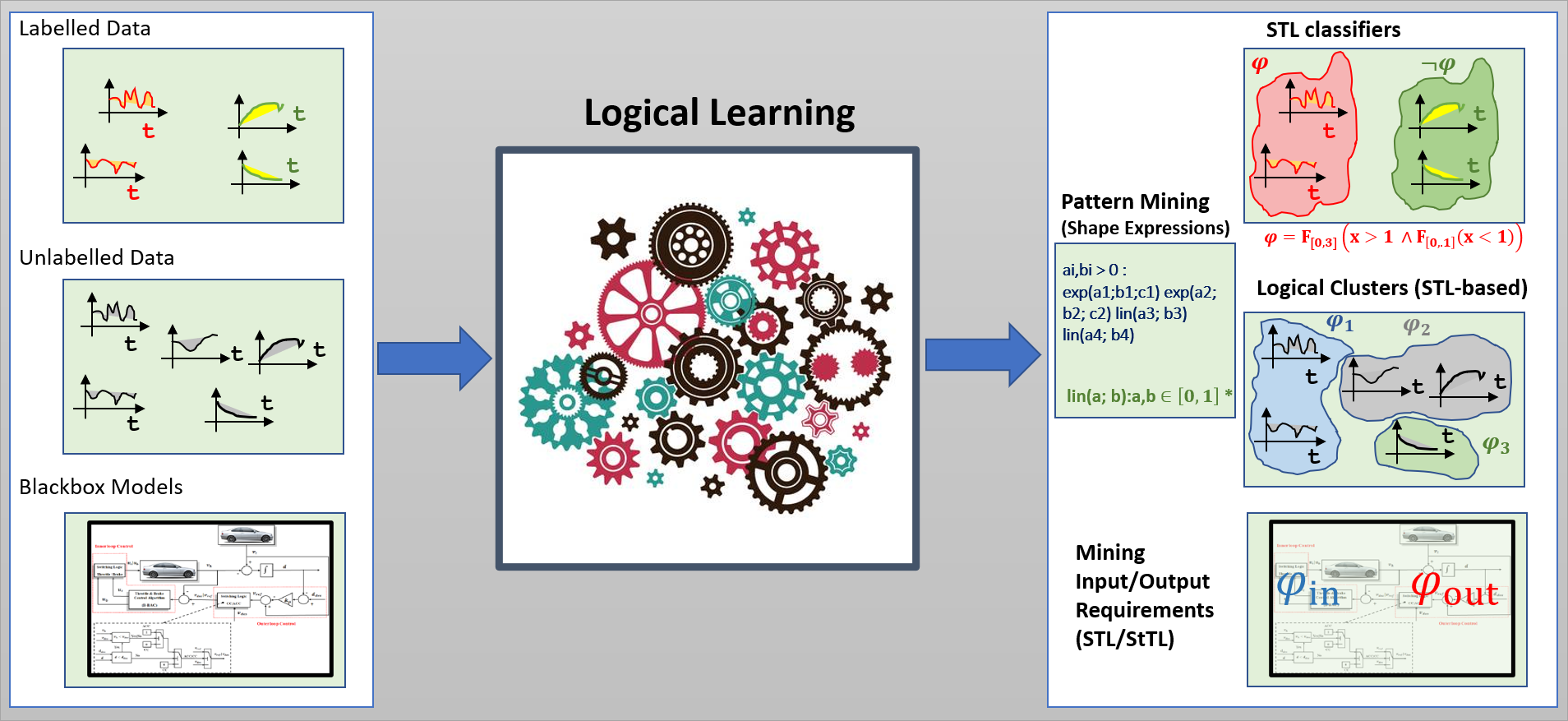
Numerous machine learning techniques have been proposed for supervised learning (classification), unsupervised learning (clustering), causality analysis, and anomaly detection for time-series data. These techniques are very powerful, giving highly accurate results for large data-sets. However, the results of learning may not always be interpretable (e.g. what do all data belonging to a particular cluster have in common? or why does the decision boundary separate two given examples). We explore the use of formal logics for supervised classification, unsupervised learning, mining information from positive examples, and mining requirements from cyber-physical system models. Specifically, we focus on learning Signal Temporal Logic formulas from data, and develop the new formalism of Shape Expressions for these tasks.
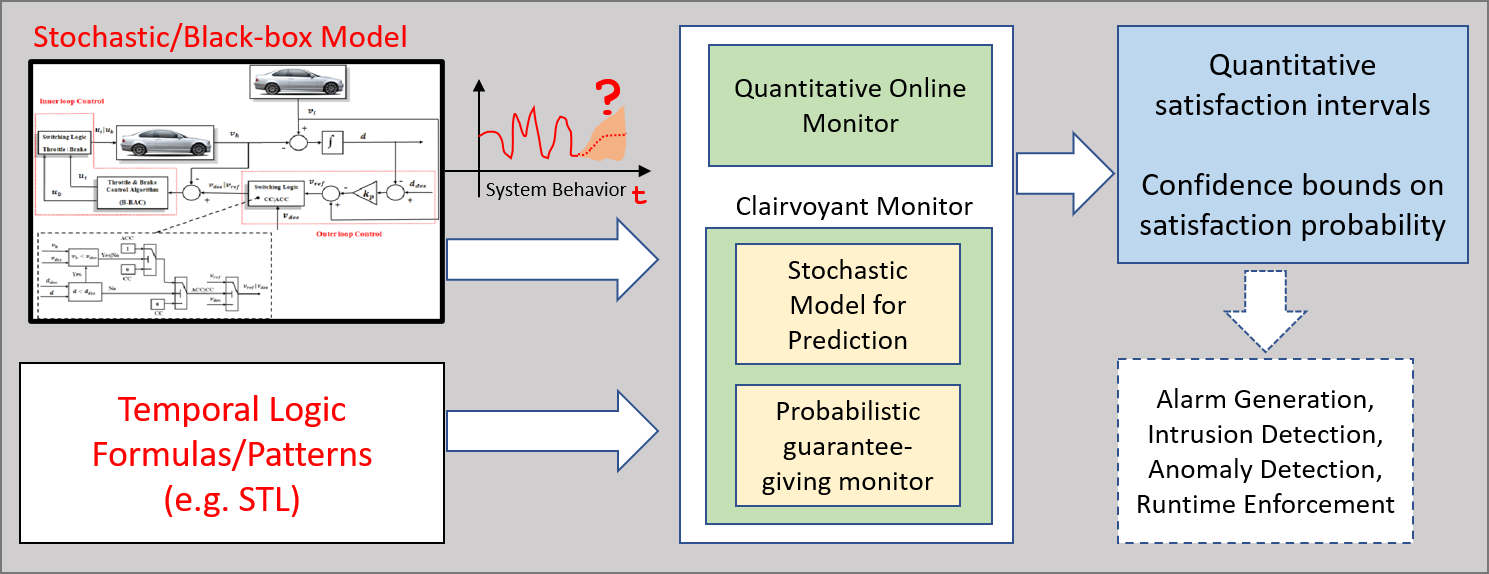
Cyberphysical systems such as autonomous aerial and ground vehicles, industrial control systems, medical devices, power grids and many others are highly complex. In very limited scenarios, formal verification techniques can digest the scale and complexity of such techniques, and even then verification guarantees correctness of a software model of the system, and not the actual deployed system. Runtime monitoring is a valuable tool to check dynamic correctness of such systems, and coupled with runtime safety enforcement can be a powerful method to assure system correctness. In particular, we are interested in monitoring temporal and logical requirements of such systems. There are several flavors of monitoring: offline or batch monitoring records temporal data about the system behaviors and runs (asynchronously) runs monitoring algorithms on the recorded data. Online monitoring checks past-time or future-time temporal logic formulas synchronously with the system. Predictive monitoring or hidden state monitors check satisfaction/violation of temporal logic formulas on hidden system states by only looking at the observable behaviors. Finally, clairvoyant monitoring is about monitoring future-time temporal logic formulas on predicted system behaviors.